おはようございます。
山本です。
突然ですが、こういうケース見てください。
- ■これまでの経験から転職に成功させた求職者のデータと求人票のデータがあり、なんとなく人の感覚で「この人、転職成功できそうだな〜」と感じる感覚
- ■ブライダルプランナーで長年の経験から、いくつかの質問をするだけで、「あ、この人はたぶんこのプランだと成約する」と直感的にわかる。
- ■結婚相談所で、これまでの経験からどういう人を紹介すれば成約するか長年の経験からわかる。
- ■旅行のプランが、その人のプロフィールを見るだけでなんとなくこれまでの経験から、提案できる
- ■MEOの順位において、何となくこのパラメーターなんだろうな〜ってものがわかっていてるもののそのパラメータの係数と演算子までは想像できない。でも確実に関係があると確信してる
- ■CVにいたるパラメータが複数確定できそうだけど、感覚的にはわかるものの、どれが本当に効いているのかわからない、でも確実にどれかは効いていると確信しているとき
人の感覚やマッチングシステムでの累積は機械学習で行える時代になりました。
特徴選択問題というものから機械学習の道がはじまります。
特徴選択問題簡単にいうと、
データセットD= {(x1,y1),(x2,y2)…}が得られたとするときに、 このとき特徴量(a.k.a.特徴ベクトル,説明変数) R^n∋ X のうち,目的変数 R∋y の説明にとって重要な項を選択せよ。
って問題に置き換えることができるということです。
「全然わかんねーよ」って人いると思います。
まずは私が作ったこちらの創作寿司をご覧ください。
(私はダイエット中のため食べれません)

落ち着きましたでしょうか。
もう少し噛み砕きますと、
x1というのはn次の関係要素だと思ってください。
x1というと一つだと思えてしまいますが、
実際は目的(目的変数)であるyiに対応する複数のパラメータを総称してxiと置いてると思ってください。
例えばレストラン店の売り上げに関係するパラメータが
「地域,ジャンル,駅までの距離,食べログ評価,インスタフォロアー数,投稿頻度,検索時のヒット数,店主の気分」などが効いてるなと思うならxはもうそのベクトルだと思ってください。49番目の店舗のパラメータは(それぞれの項目がベクトルになってるという前提で)
x49 (13,1,300,4.4,1000,5,10000,10)って感じです。
i番目なので、xiです。
わかりますよね。
そもそもそのパラメータを教えてくれよw
そうですね。その気持ちも分かりますが。
それは「教師なし学習」というものなので、今は置いておきましょう。
今は人が経験によりパラメータがわかっていたり、高い洞察力をもった人間により見抜きがある状態だとします。
これでも、様々なところで有効なケースです。
このような目的を成り立たせる要素があるとき、
目的を目的変数、成り立たせる要素を説明変数といいます。
説明変数のことを特徴量ともいいます。
そしてその特徴量の関連度を調べていく方法を「特徴選択問題の解法」といいます。
今からそれを解説していくのですが、
まずは落ち着くためにこれをご覧ください。

真鯛の漬け寿司と椎茸の漬け寿司。
(くっそうめぇと言いたいところですが今ダイエット中のため見るだけにとどまります。)
落ち着いたところで「特徴選択問題の解法」について書きます。
「特徴選択問題の解法」は2種類の方法群あります。
①モデルフリーの手法(強い仮説にのっとったやり方がない)
②モデルベースの手法(強い仮説にのっとったやり方を使う)
もう少し細かく見ると
①1. 単変量統計(フィルタータイプ特徴選択)
②1.モデルベース特徴量選択(組み合わせ型特徴選択)
2. 反復特徴量選択(ラッパータイプ特徴選択)
って感じです。
今回は①を重点的に説明します。
①単変量統計(フィルタータイプ特徴選択)の”モデルフリー“とは、一言でいうと「どのような統計モデル,回帰モデルを使うかと無関係に 変数間の関係または変数単体が一般に満たすべき基準をチェックし 不要な変数を除外していく方法」
です。
さきにこっちを解説します。
そもそもこれまでに数学をベースにした工学の世界では、
「このようなケースは、この数式にかけることで結論がでる」
というような強力な武器をもっています。
例えばエクセルなんかでも「近似曲線」とかありますよね
ちょっと正確ではないんですが
値が多少バラバラでも近似曲線を算出するロジックがあるように、さまざまな分散を扱う方法(モデル)をもってるんですね。
モデルフリーは、そのモデルを使わないということなので、
いったんそのようなお決まりのモデルを使わずに、
「ふむふむ、データ取ったのね、でもそのデータの中で、この組み合わせって他の影響を考えると無関係だよ?」と明らかにして除去をしていく方法というものです。
上の例だと
「地域,ジャンル,駅までの距離,食べログ評価,インスタフォロアー数,投稿頻度,検索時のヒット数,店主の気分」
でいうなら「店主の気分」とかマジでどうでもいいので、
これが、売り上げに比較的関係ないよ(もしくはそれを前提とすると説明できないことになるよ)というものを明らかにしてくれるという感じです。
店主の気分くらい明らかだと分かりやすいんですが、
実はインスタのフォロアー数とかが関係あると思っていたけど
実際に学習してみたら関係なかったというようなことが全然起こり得ます。
このように、説明変数(説明に使うパラメータ)として相応しくないものを除去していく手法ということです。
どのような方法で説明変数として相応しくないものを除去するか
それは、例えば、分散がゼロものは除去していいよねという考え方です。
数学的にいうと、Var[xk] = 0 とか Var[xk] がほぼ 0とか。
そういうときです。
ちなみに分散は
10 21 42 23 21 34 53 21というデータがあるときに、
この平均からそれぞれのデータを引いて和算して、データ数で割ってから二乗したものが分散です。
それがゼロってことはつまり
10 10 10 10 10 10みたいなデータのことですね。
実際はF検定などを使って除去することも多いです。(pythonのパラメータならcf. sklearn…..f_regression)
多共選性を持つものもいらね。
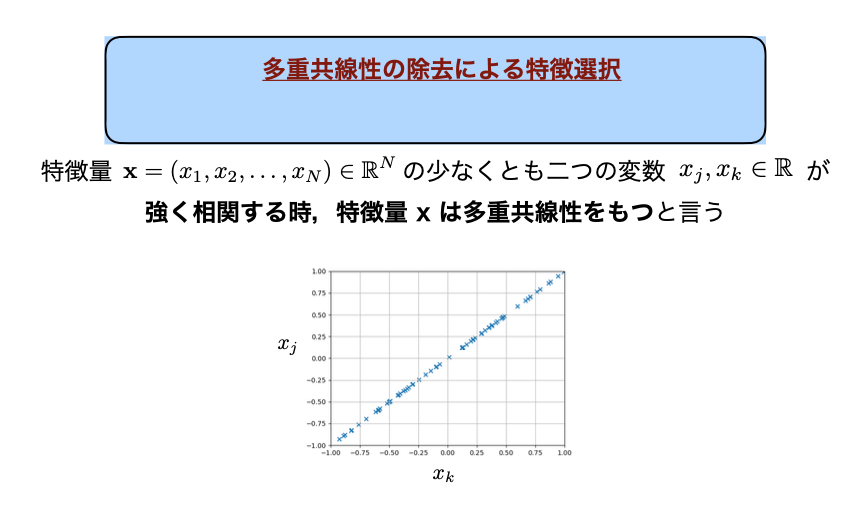
説明変数として入ってる変数同士がここまで強い比例関係があるなら、
確かに分散を考える上では一つでいいでしょうwって話です。
この多重共線性を発見する方法はvariance inflation factor (VIF)という方法で発見できます。
はい、モデルフリーのやり方はこれらがデファクトスタンダードです。

モデルフリーの説明が終わったところで素麺を食べまして
(わたしはダイエット中のため見るだけですが : 2回目)
次にモデルベースの手法を解説します。
追記中…

 事業グロース
事業グロース
